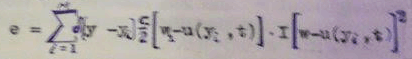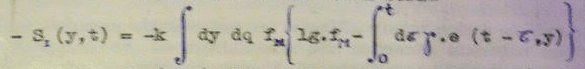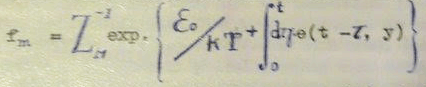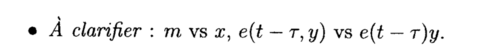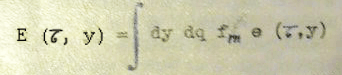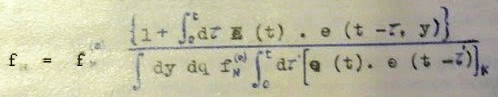E25-D612 : Différence entre versions

Version du 25 avril 2025 à 13:13

E25-D612 en PDF sur Ummo-Sciences

Impossible de télécharger le fichier en .tex, je l'ai donc copié en TXT sur la page "discussion", avec des risques d'erreurs

Page isolée

De quoi s'agit-il?

• Titre de la lettre : Extrait de lettre possiblement oummaine de 1964 dans la revue "2001"
• Date : L'article signale "la page photographiée que je vous envoie correspond à une monographie qui fut reçue à Monterrey, Mexique, le 8 octobre 1964."
• Auteur : Possiblement Oummain
• Destinataires : Le Directeur de la revue "2001" (pour ce qui est de la photocopie de cette page), et n professeur de physique à Monterrey (Mexique) (pour ce qui est du document original)
• Langue d'origine : Espagnol

Notes :Ce document provient de deux sources différentes. Il s'agit d'abord d'une photocopies de la "Revue 2001", n°20, publiée en Mars 1970 à Buenos Aire qui serait une page, élément partiel d'un soi disant rapport oummain qui aurait été reçu le 8 octobre 1964 par un professeur de physique à Monterrey (Mexique). Ce document a, par la suite, été retrouvé dans les archive de José Luis Jordán Peña.

C'est la seule page que nous ayons (et ce pour les deux sources), et elle est clairement rattachée aux courriers de l'époque : tampon, l'expression IBOSOO UU et surtout un idéogramme que l'on a retrouvé dans des lettres postérieures (modulo la symétrie), associé à un numéro comme dans d'autres lettres... Cette page semble vraiment de la source mais c'est la date du 7 octobre 1964 qui n'est pas établie avec certitude. Elle ne peut donc servir de preuve de lettre antérieure à "l'époque Sesma".

Tout ce qui concerne cette page, bien que très vraisemblable, devrait être mis au conditionnel. Ce n'est en tout cas pas "utilisable" comme preuve de date de réception d'une lettre oummaine indiquée reçue à Monterrey, Mexico, le 7 octobre 1964.

De même que ne le permettent pas les indications dans l'article : "Cela me permet d'affirmer catégoriquement avec des preuves incontestables, que Don Fernando Sesma a eu seulement un accès accidentel à l'affaire Ummo quand elle était déjà "en train de cuire" des années avant dans des cercles très restreints, au sein d'autres pays (Mexique en 1964, Australie 1964, France 1959, Canada 1963, Espagne 1965, U.S.A. 1963). C'est au moins d'alors que datent les références vérifiées que je possède.".

Au début des années 2000 (le 14 juillet 2011 d'après Jean Pollion, en 2008 d'après Manuel), Manuel Rotaeche alors en visite chez José Luis Jordan Peña discute avec Pena qui lui dit qu'il possède des documents oummains non publiés. Pena sort alors un dossier et l'ouvre, et sur la première page, Manuel reconnait ce document qu'il a rapidement le temps de photographier avec son téléphone portable. C'est grâce à cette photographie, de meilleure qualité que la photocopie du journal, que la traduction et la transcription des formules mathématiques ont pu être améliorées. On déplorera que sur la photo de Manuel, une bande de papier avec le texte "inédit", ainsi qu'un cadrage hatif, cache une partie du texte.

Témoignage de Manuel : Vers 2008 je me suis rendu chez José Luis Jordán Peña pour l'interviewer. Comme toujours il insistait être l'auteur de tout le dossier OUMMO et affirmait même avoir des lettres inédites qu'il avait finalement décidé de ne pas envoyer. Alors je lui ai demandé de me montrer un bout d'une de ces lettres. Il a donc sorti des feuilles groupées dans un dossier plastique. Il ne m'a permis de voir que la première page. Sans lui demander sa permission, j'ai pris une photo avec mon téléphone mobile. Il ne s'est pas opposé à mon action. J’ai immédiatement reconnu la lettre E25. Je lui ai dit (à Peña) que cette lettre n’était pas inédite mais qu'elle avait été envoyée à un professeur de l'université de Monterrey au Mexique. Peña est alors resté muet pendant quelques secondes, comme en réfléchissant. Au bout d'un moment il a pris le dossier, il a tout gardé et il est passé à un autre thème sans plus vouloir parler de ce sujet.

Note de J.Pollion: "Le rapport devrait comporter au moins 24 illustrations. Tampon lisible.".

Suite à la photographie de Manuel, le comité LNC a été consulté pour savoir si cette lettre devait être reclassée, soit en D612 tout simplement, ou en H dans le cas où on imagine que Pena en serait l'auteur. Finalement 5 votants on voté pour un classement D612, et 6 votants ont préféré garder le classement E25-D612. Malgré leur votes, aucun des votants ne semble avoir émis des doutes sur l'origine Oummaine de ce document, malgré sa présence dans les dossiers de Pena.

Les équations

Voici les images: elles sont difficiles à décrypter mais avec l'aide de GROK, nous avons obtenu quelques résultats. => Téléchargement de ce fichier de GROK Fichier:D612.pdf

Nous pouvons remarquer que certaines équations ont été "préparées" à la machine et complétées à la main.

Pour chaque équation vous trouverez en seconde image la proposition de GROK et ensuite d'autres proposition qui complètent parfois

Equation 4

Sapo; Selon une autre équation (plus haut, dans la lettre), la fonction « e » serait la magnitude des « flux énergétiques thermiques » et τ un « intervalle de temps élémentaire » (arbitraire).

Intéressant de voir que l’information dépend du temps et de l’énergie.

Equation 5

Equation 6

Note de Sapo Revolution: Il est intéressant de noter que le « flux informatif » fm a une forme analogue inverse à celle d’une Constante de vitesse (C) de réaction chimique, selon la Loi d’Arrhenius : Fm = 1/C, avec C=A*exp(-E0/(RT)) avec C exprimé en 1/s. Donc Fm exprimé en secondes.| L’existence de cette intégrale impliquerait qu’à une température infinie (quand le terme ε0/(kT) devient nul), le « flux d’informations » fm convergerait vers une valeur fixe (asymptote) qui dépend des variables t (temps), τ (retard ou délai ?), γ et y (variables inconnues).| La virgule, à l’intérieur de la parenthèse de e(t-τ,y) semble indiquer que e est une fonction bivariée de t-τ et de y, et non pas la fonction exponentielle (sinon, les auteurs l’auraient notée « exp », comme ils l’ont fait juste avant). | Dans cette équation de la lettre supposée U, la constante k (sous la barre de fraction) serait assimilée à R, la Constante des gaz parfaits (environ 8,3145 Joules/mol/°Kelvin). T serait la température en degrés Kelvin. ε0 serait l’équivalent d’une énergie d’activation (en J/mol).|  Quant à ZM, il serait assimilé au facteur pré-exponentiel A de la Loi d’Arrhenius. Par analogie, ZM équivaudrait au nombre d’informations bien transmises par seconde entre un transmetteur et un récepteur  - chaque transmission pouvant mener à une bonne réception ou à rien du tout | En ce qui concerne l’intégrale de temps, à l’intérieur de la fonction exponentielle, je n’ai aucune idée de ce qu’elle représente. L’indice différentiel dτ, juste derrière le signe de l’intégrale, semble indiquer que les termes γ*e(t-τ,y) ne sont pas contenus dans l’intégrale.| 

Equation 7

.

Equation 8

Equation 9

Analyse des équations par GROK