Système duodécimal : Différence entre versions
(+) |
(+) |
||
| Ligne 1 : | Ligne 1 : | ||
| − | Les Oummites utilisent le '''système duodécimal''' (système de numérotation en '''base 12'''). Ou la ''base réelle'' d'UMMO, comme ils l'appellent (D71). | + | Les Oummites utilisent le '''système duodécimal''' (système de numérotation en '''base 12'''). Ou la ''base réelle'' d'UMMO, comme ils l'appellent ({{l|D71}}).<br> |
{{lettre|D21|En [[mathématique]], nous utilisons un système de numérotation en '''base 12''' (mais nous n'avons que ''dix doigts'' comme vous). Les raisons sont purement historiques.}} | {{lettre|D21|En [[mathématique]], nous utilisons un système de numérotation en '''base 12''' (mais nous n'avons que ''dix doigts'' comme vous). Les raisons sont purement historiques.}} | ||
| + | :La base 12 : les dizaines sont multipliés par 12, les centaines sont multipliées par 12x12, les milliers par 12x12x12, etc. | ||
== Historique == | == Historique == | ||
| Ligne 13 : | Ligne 14 : | ||
:En effet, sur [[Terre]] on utilise la base 10 ''([[système décimal]])'' et quand on écrit, par exemple, '''3259''', on sait que '''3''' représente 3x1000 ('''3'''x10x10x10), '''2''' représente 2x100 ('''2'''x10x10) et '''5''' est multiplié par 10 ('''5'''x10). | :En effet, sur [[Terre]] on utilise la base 10 ''([[système décimal]])'' et quand on écrit, par exemple, '''3259''', on sait que '''3''' représente 3x1000 ('''3'''x10x10x10), '''2''' représente 2x100 ('''2'''x10x10) et '''5''' est multiplié par 10 ('''5'''x10). | ||
:Sur [[Ummo]] ils utilisent la base 12 ''('''système duodécimal''')'' : les milliers sont multipliés par 12x12x12, les centaines sont multipliées par 12x12 et les dizaines par 12. | :Sur [[Ummo]] ils utilisent la base 12 ''('''système duodécimal''')'' : les milliers sont multipliés par 12x12x12, les centaines sont multipliées par 12x12 et les dizaines par 12. | ||
| − | :On ne retient que les chiffres multipliés. '''29''' arbres = | + | :On ne retient que les chiffres multipliés. '''29''' arbres = '''2'''x12 + '''5''' ; les oummites écrivent 2 ([[IEN]]) et 5 ([[IEGO]]) : «[[Fichier:02-I·EN.png|15px]][[Fichier:05-I·EGO.png|15px]]». |
== Ordinateurs (XANMMO BAA) : codification duodécimale == | == Ordinateurs (XANMMO BAA) : codification duodécimale == | ||
Version actuelle datée du 15 mai 2019 à 11:40
Les Oummites utilisent le système duodécimal (système de numérotation en base 12). Ou la base réelle d'UMMO, comme ils l'appellent (D71).
- La base 12 : les dizaines sont multipliés par 12, les centaines sont multipliées par 12x12, les milliers par 12x12x12, etc.
Sommaire
Historique
Base 12
Notre système de NUMÉRATION est de base 12, alors que vous avez, vous, choisi un système décimal. En dehors du fait logique selon lequel les signes employés par les terrestres sont différents, les expressions des différents nombres complexes s'effectuent en ordonnant les chiffres de la même manière que vous. Cependant celui qui n'est pas familiarisé avec ce système de numération à base 12 peut trouver étrange que pour écrire une quantité de 29 arbres par exemple, il faille en réalité écrire 25. N'importe lequel de vos mathématiciens résoudra cette contradiction apparente.
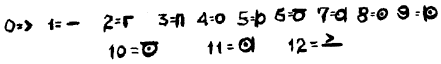
- En effet, sur Terre on utilise la base 10 (système décimal) et quand on écrit, par exemple, 3259, on sait que 3 représente 3x1000 (3x10x10x10), 2 représente 2x100 (2x10x10) et 5 est multiplié par 10 (5x10).
- Sur Ummo ils utilisent la base 12 (système duodécimal) : les milliers sont multipliés par 12x12x12, les centaines sont multipliées par 12x12 et les dizaines par 12.
- On ne retient que les chiffres multipliés. 29 arbres = 2x12 + 5 ; les oummites écrivent 2 (IEN) et 5 (IEGO) : «
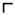
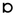 ».
».
Ordinateurs (XANMMO BAA) : codification duodécimale
BASE OPÉRATIONNELLE
Il est certain que si vous utilisez des valvules électroniques ou des transistors dans vos circuits, il faut alors un type de codage que vous appelez BOOLÉEN du type TOUT- RIEN […] ZÉRO - UN. Les unités arithmétiques travaillent avec un meilleur rendement et un degré de fiabilité que vous n'obtiendrez pas en employant votre système de base 10.
Ainsi des opérations en système binaire comme :
101 + 111 = 1100
(5) + (7) = (12)
peuvent nécessiter, si les chiffres sont élevés, un grand nombre de bits pour être exprimés.
Les unités IYOAEE BOO et les XANWAABUUASII (MÉMOIRES DE TITANE) peuvent par contre opérer en base réelle d'UMMO (c'est-à-dire : 12) […].Circuits de calcul (IYOAEE BOO)
Pour cela nous employons quelques centaines de ces réactions basiques, choisies spécifiquement, pour que les nombres simples utilisés soient exprimés en système de base 12.
Par exemple, la codification de cette addition : 12 + 1 = 13
et la vérification correspondante se réalise au moyen de cette réaction : C12 6+ H11 = N137 (image S71-f3)
Dans laquelle interviennent des micromasses parfaitement contrôlées et non pas des billions d'atomes comme si les masses en réaction étaient grandes.
Mémoires de données en titane (XANWAABUASII)
Problème de conversion
Vous devez rectifier la valeur, indiquée à tort, de 2100 x 1400 kilomètres par la valeur 2100.123 x 1400.123 mètres.
- Cette valeur correspond à l'arrondi approximatif de la valeur exacte de 420 x 276 KOAEE, soit environ 3660 x 2400 x 106 mètres carrés.
Liens
- Chiffres et nombres
- www.oumo.fr : Page pour convertir des chiffres et nombres terriens en oummains (oummites)
- Wikipédia : Système duodécimal